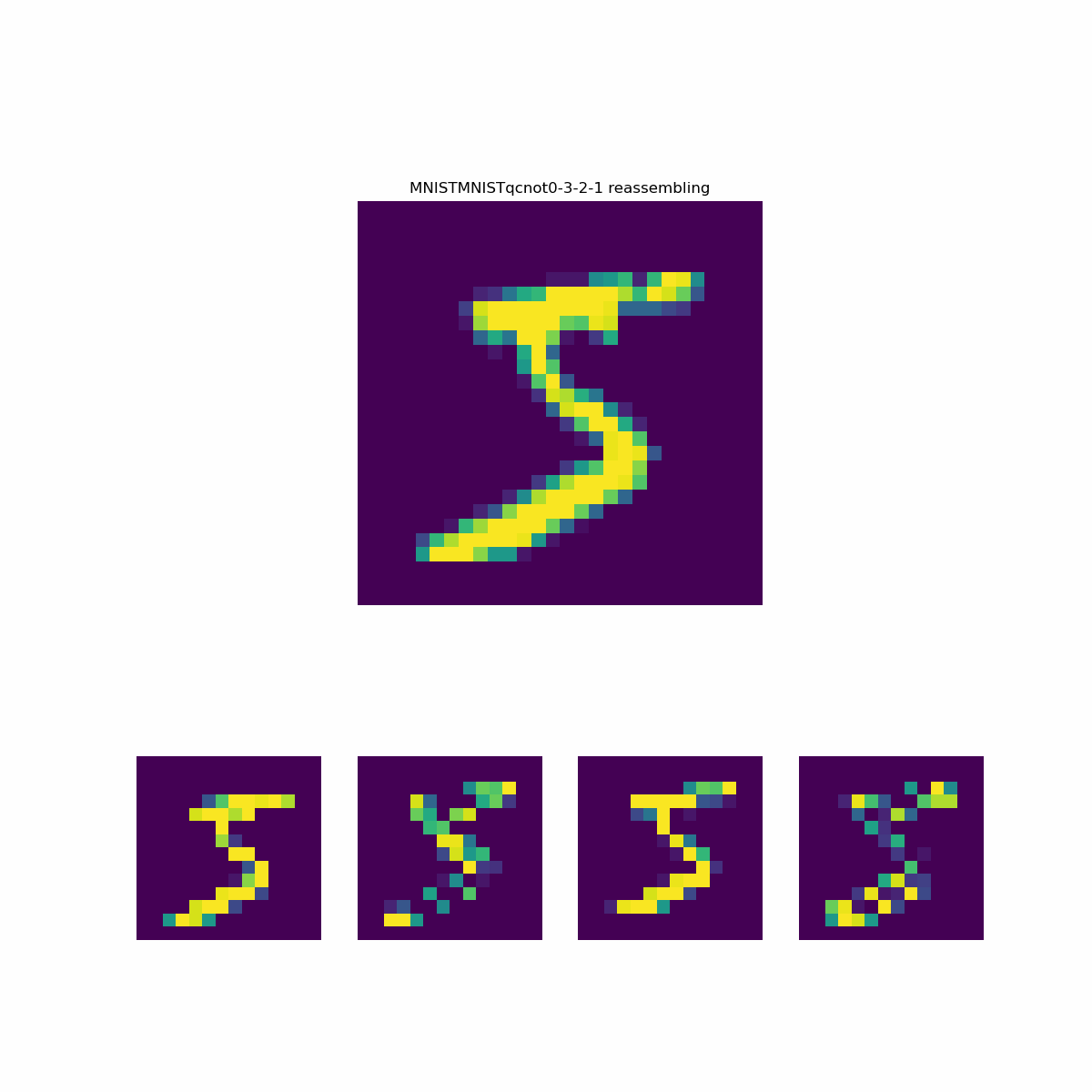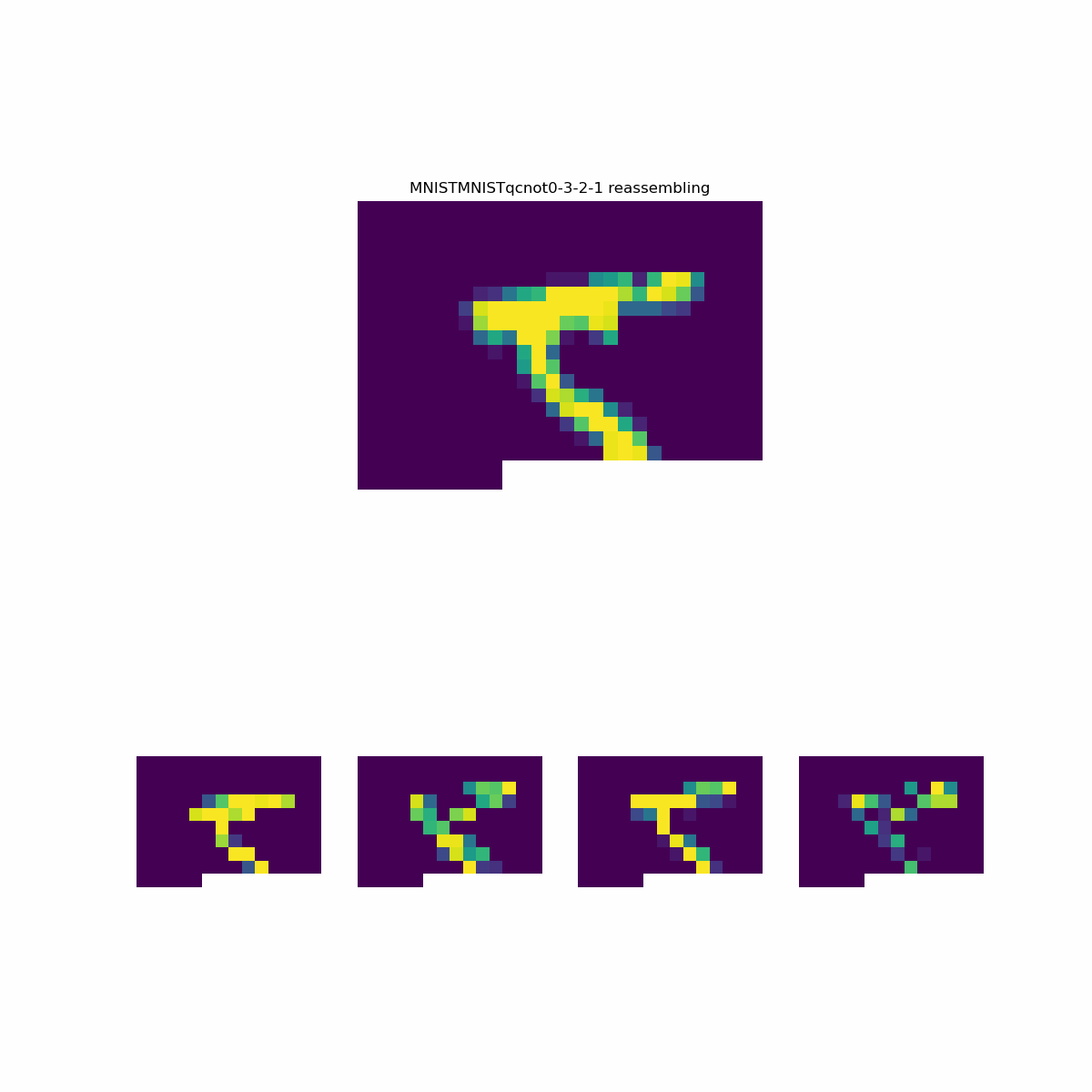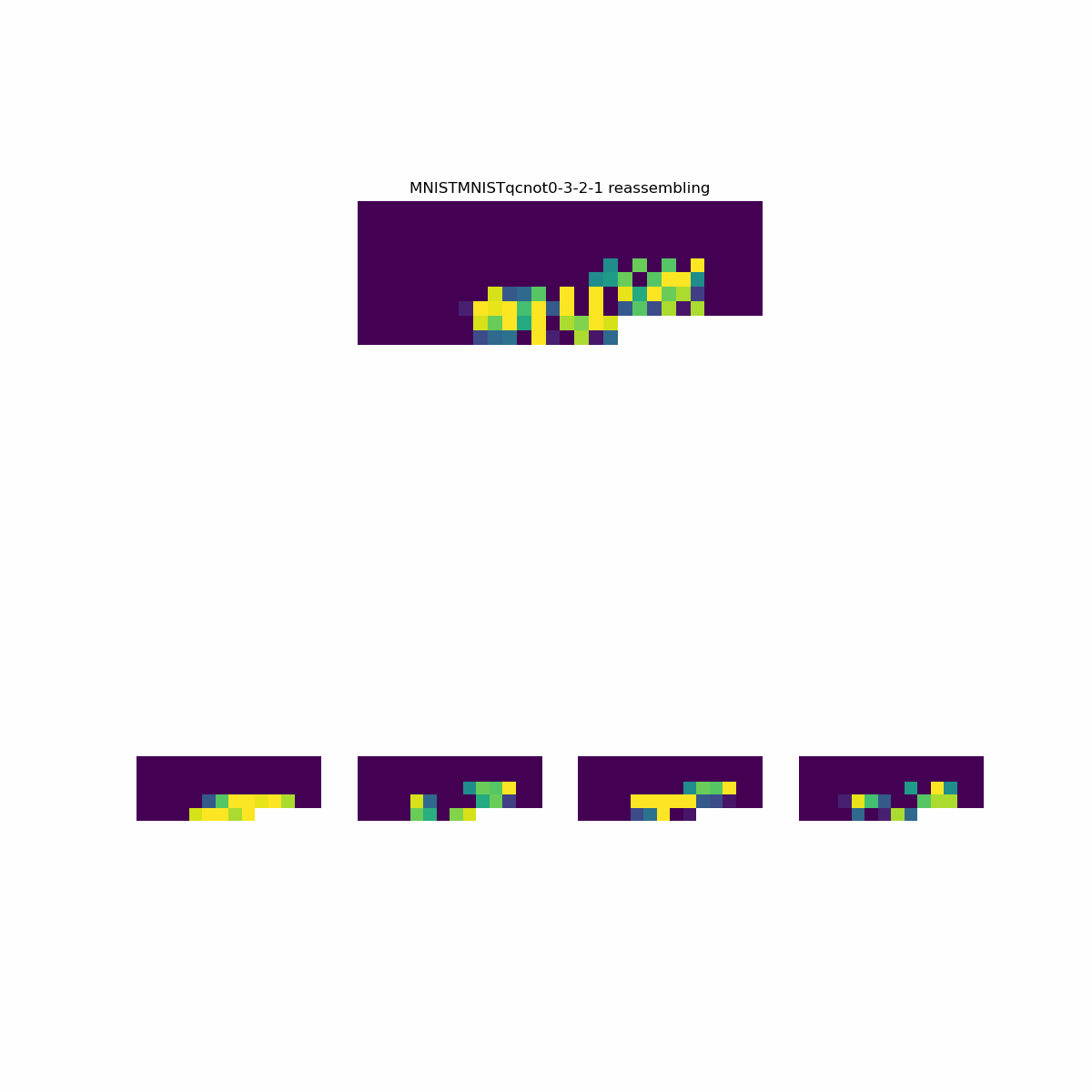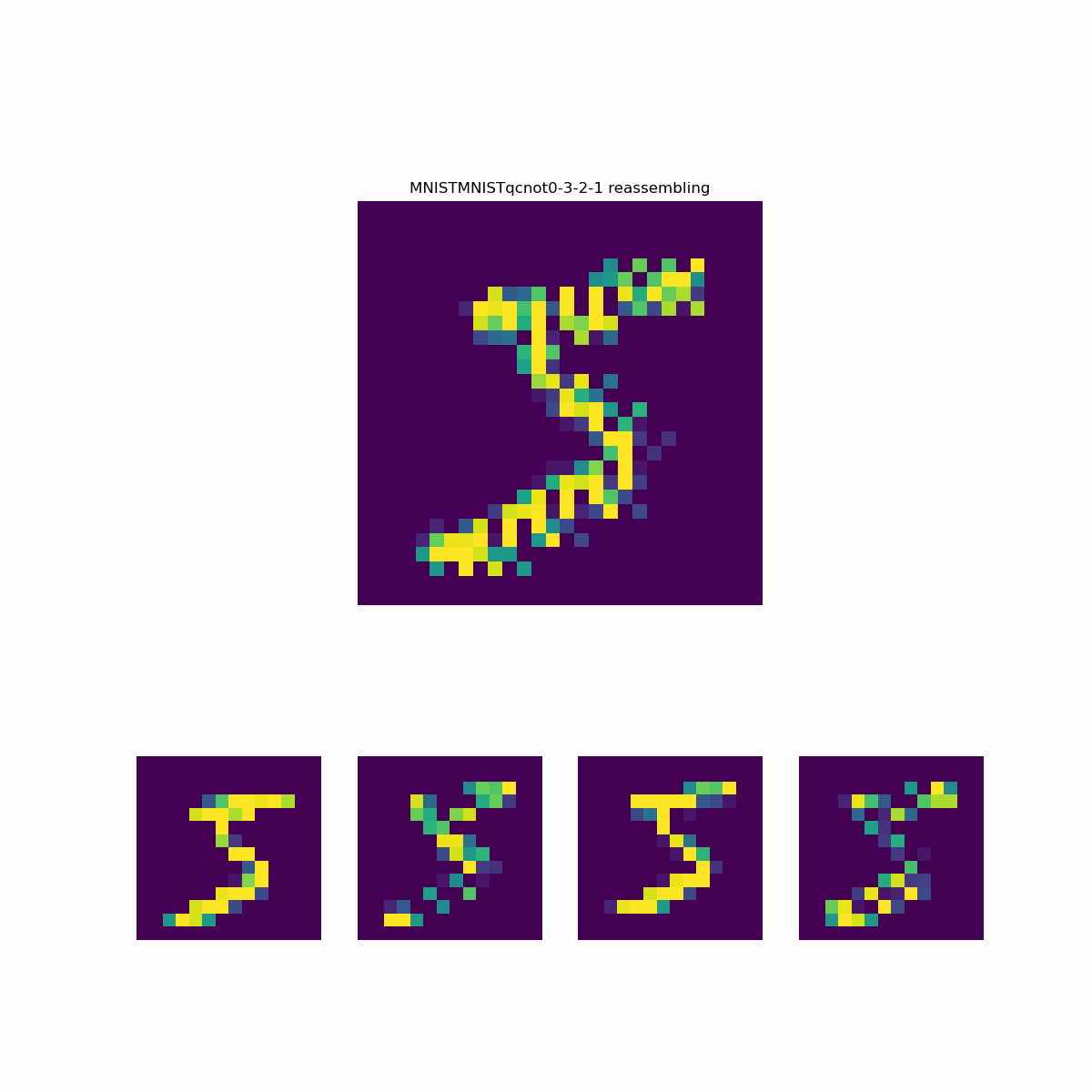Quantum Pre-Processing Filters for Machine Learning

My previous projects exploring quantum feature space left me with more questions than answers. Recently I was given the opportunity to learn and run experiments with Quantum Machine Learning mentor Carlos Kuhn, the Research Chair of University of Canberra's Open Source Institute. This opportunity was made possible by the Quantum Computing Mentorship Program provided by the Quantum Open Source Foundation. Each cohort they offer requires a submission including work on an assessment task. I really wracked my brain on this one. Thankfully, Carlos and some other mentors liked my assessment task submission.

The work lead by Carlos was inspired by the paper Application of Quantum Pre-Processing Filter for Binary Image Classification with Small Samples. The paper portrays improvements in training outcomes on a simple network when one or two quantum operations are applied as preprocessing on the MNIST dataset. However, no solid explanation is really made on the mechanisms at play that increase the training accuracy. 

A related paper Quanvolutional Neural Networks: Powering Image Recognition with Quantum Circuits is the basis for a PennyLane demonstration on using Quanvolutional Neural Networks. The demo is a great resource for hands on experience with quantum machine learning. This helped me get familiar with PennyLane, Keras, and Tensorflow.

The core of our experimentation was set up similarly to the demo and we collected data on various changes and alternative preprocessing filters. As experiments and variations grew, collecting data on their impacts became more time intensive. Once experimentation advanced to larger sample sizes the time intensity delayed the respective data analysis and data informed future experimentation. Put more simply, it took hours to complete preprocessing and training on the full MNIST dataset.

In the paper, the quantum preprocessing is done on grayscale image values scaled to the range [0,1]. The images are 28x28 pixels, that is a 14x14 set of 2x2 squares. Each 2x2 square containing four values. In the quantum circuit, the four values are angle embedded on four wires. The best performing two-operation circuits consisted of CNOT operations on both diagonal pairs in the 2x2 section. The diagonal pairs are on wires (2, 1) and (0,3). Each wire is measured into a different channel resulting in 4, 14x14 images per sample. The preprocessed images are used to train a Keras model with a flat layer followed by a dense layer.

def quanv(image):
    """Convolves the input image with many applications of the same quantum circuit."""
    out = np.zeros((14, 14, 4))

    # Loop over the coordinates of the top-left pixel of 2X2 squares
    for j in range(0, 28, 2):
        for k in range(0, 28, 2):
            # Process a squared 2x2 region of the image with a quantum circuit
            q_results = circuit(
                [
                    image[j, k, 0],
                    image[j, k + 1, 0],
                    image[j + 1, k, 0],
                    image[j + 1, k + 1, 0]
                ]
            )
            # Assign expectation values to different channels of the output pixel (j/2, k/2)
            for c in range(4):
                out[j // 2, k // 2, c] = q_results[c]
    return out

Using the looping in the demo on the full dataset would mean linearly through and applying the quantum circuit to each 2x2 segment in each 28x28 image in a set of over 10000 images. This isn't optimal.

#14x14 flattened 2x2 squares
get_subsections_14x14 = lambda im : tf.reshape(tf.unstack(tf.reshape(im,[14,2,14,2]), axis = 2),[14,14,4])

#unpack 14x14 row by row
list_squares_2x2 = lambda image_subsections: tf.reshape(tf.unstack(image_subsections, axis = 1), [196,4])

#send 4 values to quantum function
process_square_2x2 = lambda square_2x2 : self.q_node(square_2x2)

#send all squares to the quantum function wrapper
process_subsections = lambda squares: tf.vectorized_map(process_square_2x2,squares)

#recompile the larger square
separate_channels = lambda channel_stack: tf.reshape(channel_stack, [14,14,4])
#each smaller square (channel) can be extracted as [:, :, channel]

#apply function across batch
lambda input: tf.vectorized_map(
    lambda image:(separate_channels(tf.transpose(process_subsections(list_squares_2x2(get_subsections_14x14(image)))))),input)

Using the TensorFlow qubit device in Pennylane opens up the ability to apply quantum circuits as vector operations in TensorFlow. Using a custom Keras layer and and appropriately reshaping the input allowed the operation to be applied across a whole batch of images at once. This optimization allowed experiments to expand to much larger scales. Instead of waiting hours to process and then train on a larger sample we now are able to process and train 576 different filter variations on the full dataset in under 2 hours.

Our ongoing experimentation is public on the TheOpenSI's GitHub repository QML-QPF